This is the first follow-up workshop to the TGDA+Neuro Curriculum Design Workshop and the TGDA+Neuroscience Course.
Group 1: Neuro Tree Clustering (mentored by Yusu Wang)
Group 2: Neuro Tree Clustering (mentored by Yusu Wang)
Group 3: Shape Analysis and Classification via Persistent Homology (mentored by Facundo Memoli)
Group 4: Shape Analysis and Classification via Persistent Homology (mentored by Facundo Memoli)
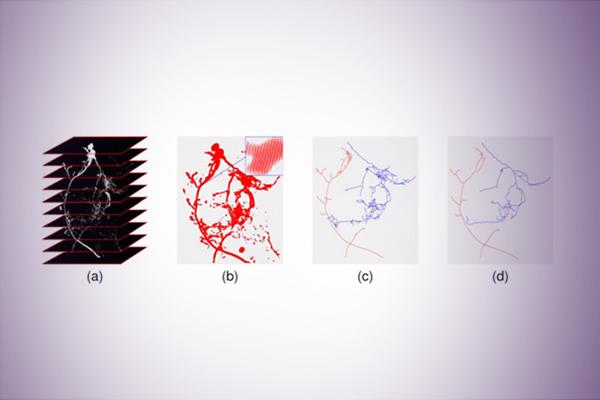
Neuro Tree Clustering
Neuron cells have natural tree morphology, rooted at the cell body (soma), with dendrite and axon branching out. Hence it is common in the field of neuroscience to model a neuron as a geometric rooted tree (with root typically at soma). In this project, we will explore how to use persistence diagram summaries to cluster neuron cells. To compare these neuron cells, we then need to compare geometric trees, which is a highly non-trivial problem. Instead, we first perform the persistent homology transfer to map each neuron tree to a certain persistence diagram in the space of persistence diagrams. Then, we will use an appropriate metric on the space of persistence diagrams to compare these neurons via comparing their persistence diagram summaries. For example, we can use the bottleneck distance introduced in class to compare the distance between two persistence diagrams, or we can use the Wasserstein distance. Finally, we obtain the distances between all pairs of input neurons, and we can use it to either perform clustering or nearest neighbor search.
Shape Analysis and Classification via Persistent Homology
This project will build upon the lectures from March 25th and April 1st. By using ideas from persistent homology, we are going to analyze and try to discriminate the different classes (dogs, cats, gorillas, horses, etc) from the Non-Rigid World TOSCA database of 3D shapes. The project will expose students to several of the challenges that arise when working with data that could be noisy, or simply too large to process all at once. This database of shapes contains nearly 150 different shapes, each of which has a few thousand points. In order to process the shapes in this database we will have to not only use efficient subsampling methods, but we will also have to resort to fast implementations of Ripser (the ``live" version will not be practical). In particular, one of the initial steps of this project will be to install Ripser in your own computer (a step which will require compiling the C++ code). We will provide instructions for doing this.
